Can science make a better music theory?

My last post discussed how we should be deriving music theory from empirical observation of what people like using ethnomusicology. Another good strategy would be to derive music theory from observation of what’s going on between our ears. Daniel Shawcross Wilkerson has attempted just that in his essay, Harmony Explained: Progress Towards A Scientific Theory of Music. The essay has an endearingly old-timey subtitle:

The Major Scale, The Standard Chord Dictionary, and The Difference of Feeling Between The Major and Minor Triads Explained from the First Principles of Physics and Computation; The Theory of Helmholtz Shown To Be Incomplete and The Theory of Terhardt and Some Others Considered

Wilkerson begins with the observation that music theory books read like medical texts from the middle ages: “they contain unjustified superstition, non-reasoning, and funny symbols glorified by Latin phrases.” We can do better.

Wilkerson proposes that we derive a theory of harmony from first principles drawn from our understanding of how the brain processes audio signals. We evolved to be able to detect sounds with natural harmonics, because those usually come from significant sources, like the throats of other animals. Musical harmony is our way of gratifying our harmonic-series detectors.

How good are we at detecting the harmonics of a sound? So good that if we hear a partial overtone series, we can effortlessly and unconsciously deduce the missing tones. For example, if we hear a harmonic series with the fundamental missing, we automatically fill in the fundamental. More specifically, if we hear a blend of tones, we can figure out the greatest common divisor of their frequencies and assume that to be the fundamental. This phenomenon of “virtual pitch” is what makes it possible to hear the bassline in a song played back on tiny earbuds. Even though the speakers aren’t physically big enough to produce bass notes, we extrapolate them anyway from their overtones.

The idea that our brains have specialized harmonic series detectors also helps explain where octave equivalency come from.

While the tones of different Harmonic Series differ, conveniently the ratio of their frequencies to their fundamental frequency does not. Therefore we consider it very likely that the brain normalizes tones by dividing tones to get tone ratios… Processing sound requires operating on frequencies over several orders of magnitude. If these frequencies could be made to “wrap-around” then we have another opportunity for code re-use. Consider the conceptually straightforward process of the brain halving or doubling the frequency of a wave until it is within a particular range. Now the brain only needs a Harmonic Series recognizer for tones within a frequency range of a single factor of two, not across the whole spectrum of sound. Breaking the problem into two parts like this, (1) normalization followed by (2) recognition, greatly simplifies the resulting frequency recognizer. We therefore consider it likely that the brain normalizes tones by halving or doubling them until within a particular frequency range spanned by a factor of two. It seems very likely that the brain is halving/doubling frequencies by many different powers of two in parallel and then running all of the results through the frequency recognizer at once. If any one matches, the harmonic has been found.

So, why do we like harmony? Wilkerson says that it boils down to artificial reinforcement of the natural overtone series. Hearing a chord is like hearing a magical voice with stronger and clearer harmonics than would be possible from a single sound source. As Wilkerson puts it, harmony is “sweeter than sweet.”

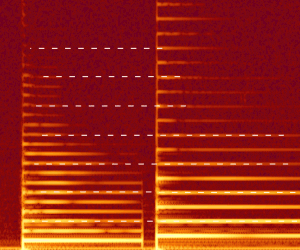
Here’s an illustration of what Wilkerson means. It shows the spectrogram of two notes played on the violin: C on the left, G on the right.

The dotted lines show that these two notes have very similar spectra. Every third overtone from C can be found identically in G. If you hear these two notes at the same time, your brain’s harmonic pattern recognizer instantly lights up showing spectacular agreement.

That’s a good explanation of consonance. But we like harmonies that are not so consonant, too. How does Wilkerson account for that? He attributes it to our inborn love of narrative, likening a sequence of chords to a story.

[I]f understanding and predicting a storyline are too easy, then it is boring, and if too hard, then it is noise, but if just right, then it is interesting… simplicity comes from data having a “theme” and ambiguity is the absence of a single explanation or theme and therefore a good way to rapidly produce complexity…

Discovering a theme in some input is a way to manage the complexity of the input. Likely layers of theme and the resulting unexplained residual complexity are being processed by an expectation engine in the brain. Much of the art of manipulating harmony is simply playing with this expectation engine, giving it just enough complexity so the input remains on the interesting border between monotony and noise.

Here’s how Wilkerson suggests that we derive simple diatonic harmony from the natural overtone series. We start by finding the ideal harmonic series of a single note, say C4 (middle C on the piano), and map it into a single octave by dividing the frequency by two as needed. I’ll follow Wilkerson’s convention and refer to the fundamental as the first harmonic.

• The second harmonic has a frequency twice that of C4, giving you C5, which is an octave higher than C4.
• The third harmonic, with a frequency three times that of C4, is G5. When you divide its frequency by two, you get G4, up a perfect fifth from C4.
• The fourth harmonic, with a frequency four times that of C4, is C6. In fact, all even-numbered harmonics are just C in higher and higher octaves.
• The fifth harmonic, with a frequency five times that of C4, is E6. Normalizing that down a couple of octaves gives us E4, a major third above C4.

There in the first few natural harmonics is the major triad, C, E and G (plus a bunch of octaves.) Any starting pitch will produce the same frequency ratios.

Next, Wilkerson has us construct another major triad based on the note in the overtone series most similar to the fundamental. The first note you get from the harmonics of C (other than C an octave up) is G. If you build a major triad from G, you get the notes G, B and D. Then Wilkerson has us start a major triad on another closely related note, the one whose third harmonic is C. That note is F, and the major triad it produces from its overtone series is F, A and C. Putting all those notes in order by frequency gives you C, D, E, F, G, A, B, the familiar major scale.

Once you have this collection of pitches, you can derive all kinds of other interesting chords and scales from it. If you use D, E or A as the root, you get minor triads. Our emotional reaction to minor chords is more complex than the simple “aha!” of recognition that we get from major. An A minor triad has the same pairwise intervals as the harmonic series: a fifth between A and E, and a major third between C and E. But we don’t hear the Harmonic Series itself. Wilkerson thinks we find minor chords interesting because of the way that they tease our inner harmonic series recognizer with partial recognition.

This theory is further re-enforced by the fact that there is one Major Scale whereas there are many Minor scales. Recall that in the Major Scale, built from the Major Triad, everything goes “right”, whereas in the Minor scales, built from the Minor Triad, something is always “off” or “wrong.”

We devote a lot of our processor power to disambiguation: finding the likeliest coherent explanation for the vague and contradictory information we have about the world. This is what makes us smarter than computers in certain ways. Computers are better at doing logic with complete information, but we’re better at making educated guesses from incomplete information. Music teases our inner disambiguation engine, giving it recognizable patterns without any obvious meaning.

Wilkerson likens complex harmony to cubist paintings:

[T]he parts of an object may be rendered reasonably faithfully so that one recognizes them, however they do not arrange into a whole in a coherent way. This produces an interesting effect: we recognize the object, as the features we require for recognition do fire, although we still have an overall feeling that we are not seeing the thing in its natural form, but instead in a disturbed or unhappy or dreamy state.

What about more complex chords? Wilkerson says that the same logic from minor chords applies generally:

The brain wants to hear one Harmonic Series. If we leave out more and more notes and the brain is filling in more and more, we can start to get really close to barely playing enough notes for the brain to figure out which Harmonic Series it is supposed to be listening to. What if we play so few notes that the implied Harmonic Series is ambiguous, that the missing Harmonic Series could be completed in more than one way?

Some chords are ambiguous therefore unstable: if we give the brain more than one alternative then the sound is is “unsettled” until the player provides enough notes to “break symmetry” and disambiguate the series.

If you hear the notes C, F and G, you hear something that resembles the natural overtone series, kind of. But which one? Either C or F could be the root here. Musicians call this is a suspended chord, which is a usefully descriptive term. You’re suspended between two possibilities, that C is the root note, or that F is. If you replace the F with an E, the suspense is resolved in favor of C. If you replace the G with an A, then the suspense is resolved in favor of F. In more modern music, the suspense may well never get resolved at all.

The ambiguity idea works well to explain any of the more exotic chords. When you hear an augmented or diminished triad, or a jazz chord with a lot of extensions, you hear pairwise intervals that are familiar from the overtone series, but you don’t hear a complete overtone series, or maybe you hear more than one. The result isn’t as directly gratifying as a major chord, but it still sounds like something meaningful; you just have to work harder to figure out what’s going on.

[I]t is likely that the brain has one disambiguation engine and that the processing that occurs in verbal narrative would process similarly in other contexts, such as music. So, while these chords may sound strange in isolation, the theme created by the preceding music before the chord may bring a certain sense to them. Think of one standard structure for a joke: a story (creating a theme) and then a punchline; the punchline would not be funny in isolation without the context provided by the story, and yet we attribute the funniness of the joke to the punchline and not the story which did the work.

Putting the harmonic series at the heart and soul of harmony mostly puts Wilkerson’s theory in agreement with standard classical theory. However, there are a few places where he diverges. For example, he dismisses the circle of fifths as a combinatorial coincidence, rather than anything fundamentally illuminating about the nature of music.

The Circle of Fifths is just a huge red herring that prevents people from understanding harmony, or at least how it is that harmony sounds good.

I like Wilkerson’s theory a lot, but there’s one place where he’s pretty much wrong, and that is his analysis of the tritone.

Play C and F# on a piano; it sounds awful. This interval is also called the Tritone as the distance between C and F# is three whole tones (where here “tone” means a distance of two semi-tones, so a distance of six semi-tones). We can see how it emerges that it sounds so bad: the ratio between F# and C it isn’t near that of any of the harmonics in the Harmonic Series. This interval deserves its nickname as the Devil’s Interval.

While Wilkerson has done a good job of liberating his thinking from his Eurocentric musical enculturation, here he lets some bias show. Those of us who enjoy the blues and its musical descendants don’t find the tritone to sound awful at all. It comes straight out of the harmonic series, you can hear it between overtones five and seven.

Like too many music theorists, Wilkerson has a lot to say about harmony and little to say about rhythm. But he does have this wonderful little paragraph:

Recently while listening to the rhythm of an insect at twilight I was struck by how the rhythm occurred in layers of declining theme and increasing complexity: there was a simple rhythm creating an expectation, and then regular a violation of that expectation, creating a rhythm on top of that. This phenomenon of narrative, of anticipation and prediction within a theme, applies to both harmony and rhythm. The phenomenon of expectation itself is likely generic across kinds of inputs and so harmonic expectation should work in a similarly layered manner as rhythmic expectation.

Just as harmony is an idealized abstraction of the human voice, so rhythm is an idealized abstraction of physical movements like walking and dancing. I’d like to take Wilkerson’s theory a step further. A pitch is a really just a very fast rhythm. Chords are very fast polyrhythm. Just as rhythm is fundamental to music generally, so too should our theory of rhythm be fundamental to our theory of music generally.